極小曲面#

極小曲面とは平均曲率が0の曲面のことである. たとえば, 座標を用いて曲面を \(z = u(x,y)\) と表すと, ラプラス方程式 \(\displaystyle \left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right)u(x,y)=0\) を満たす. つまり, \(x\) 方向に凸なら(1項が負), \(y\) 方向はそれに応じて凹こんでいる(2項が正). 決して両方一緒に凸や, 凹になることはない.
解析関数の実部, 虚部もそれぞれ極小曲面を定義する. 2次元の静電ポテンシャル \(\phi(x,y)\) も極小曲面とみなすことができる. 石鹸膜のような弾性膜もその張力のために極小曲面をなす. ここではストッキングを使って極小曲面を作ってみよう.
準備するもの
境界条件: 何でもよいが, ここでは木のブロックを使った.
表面: ストッキング
例: 直径9cmの木の円盤に, 1辺3cmの立方体のブロックをおいて境界条件を作成した. 立方体の角の部分で, 勾配が無限大になっている様子がわかる. このような特異点が簡単な系で実現できていることは興味深い。
補足#
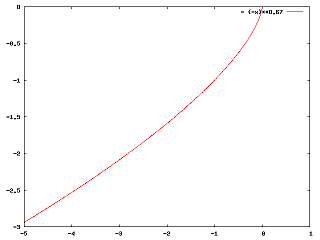
尖点のポテンシャルが、 \(\rho^{1/(2-\alpha/\pi)}\) に比例することは比較的簡単に求められる。 \(\rho\) は尖点からの距離、 \(\alpha\) は開き角である。 今の例では、\(\rho^{2/3}\) であり、勾配が無限大であることが分かる。
参考文献#
J.D. Jackson: Classical Electrodynamics, 3rd ed. (John Wiley, 1998) pp. 75–79.
