指数関数#
ネピア数 (自然対数の底) は
\[\begin{align*}
\ee := \lim_{m\rightarrow\infty}\left(1 + \frac1m\right)^m
\end{align*}\]
で定義される. 左辺において \(\nu=am\) (\(a\) は適当な数) とおくと
\[\begin{align*}
\lim_{|\nu|\rightarrow\infty}\left(1 + \frac{a}{\nu}\right)^{\nu}
=
\lim_{m\rightarrow\infty}\left(1 + \frac{a}{n}\right)^{n} = \ee^a
\end{align*}\]
が得られる. \(n\) は \(|\nu|\) に近い自然数である.
ここで, \(a=\ii\pi\alpha\) (純虚数), \(\alpha=k/n\) とおく.
\[\begin{align*}
\lim_{n\rightarrow\infty,\:
k/n\rightarrow\alpha}\left(1 + \ii\pi\frac{k}{n}\right)^n
= \ee^{\ii\pi\alpha}
\end{align*}\]
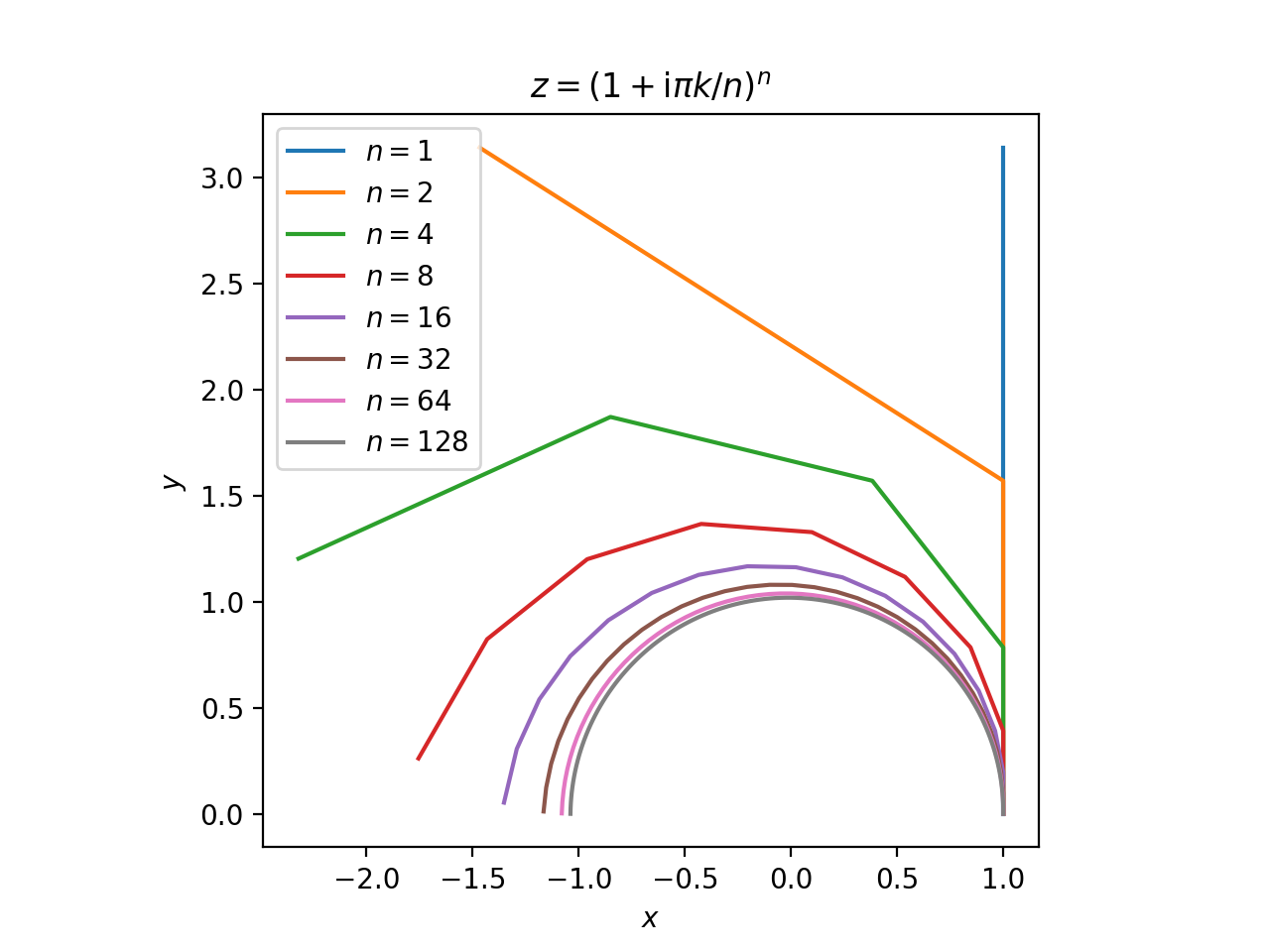
\(z_n(k)=(1+\ii\pi k/n)\) (\(k=1,\ldots,n\)) を複素平面でプロットしたものが下の図である. 半円 \(z=\ee^{\ii\pi\alpha}\) \((0\leq\alpha\leq 1)\) に近づいていることが分かる.
指数関数#
import numpy as npimport numpy as np
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.set_title(r'$z_n(k)=(1 + \mathrm{i}\pi k / n)^n$')
for i in range(0, 8):
n = 2 ** i
z1 = 1.0 + 1.0j * np.pi / n
z = np.array([z1 ** k for k in range(n + 1)])
ax.plot(np.real(z), np.imag(z), label=fr'$n={n}$')
ax.set_aspect('equal')
ax.legend()
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
plt.show()
